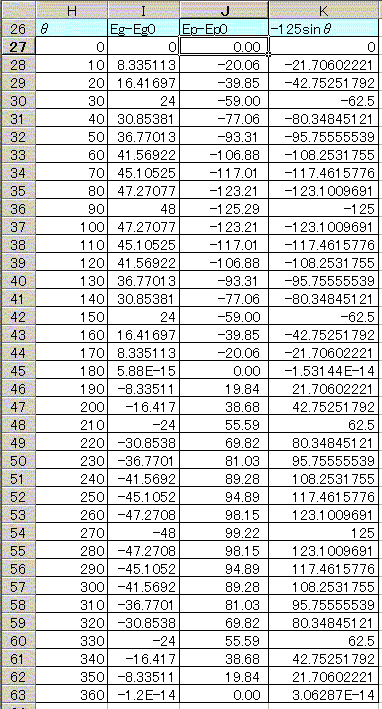
MS-Excel ��p���Đ^��ǂ�Ep�|Ip�����O���t����o�͔g�`�Ƙc�����Z�o������@
2004.11.27
2004.12.09�C��
2006.2.5�c���̒�`�����
�ڎ��F
�͂��߂��͂��߂�
�@�^��ǂ̃��[�h���C������A���͔g�`�Əo�͔g�`�̊W���v�Z���邱�Ƃ��ł��Ȃ����ƍl���A���̕������l���܂����B�ŏ��̍�肱�݂͖ʓ|�ł����A�Q��ڈȍ~�͍ŏ��̃f�[�^���݂͂̂Ō��ʂ��o��̂ő�ϕ֗��ł��B�܂��A��肱�݂̉ߒ��ŁA������p�ɂ��Ă̗�����[�߂邱�Ƃ��ł��܂����B���ۂ̉�H�v�ɗp����ɂ͉�H�V�~�����[�^�[�̂ق����f�R�֗��ł����A���[�h���C��������������g�ɂ���ɂ͕֗��ȓ���ł͂Ȃ����Ǝv���܂��B
�@�d�q�H�w�����w���S���̃A�}�`���A�ł��̂ŁA�p��̖��ȂǁA�s�K�ȕ�����l���Ⴂ�����邩�Ǝv���܂��B���C�Â��̓_�ɂ��Ă͂���������������K���ł��B�@�@
�@
Step1�F���[�h���C�����쐬����
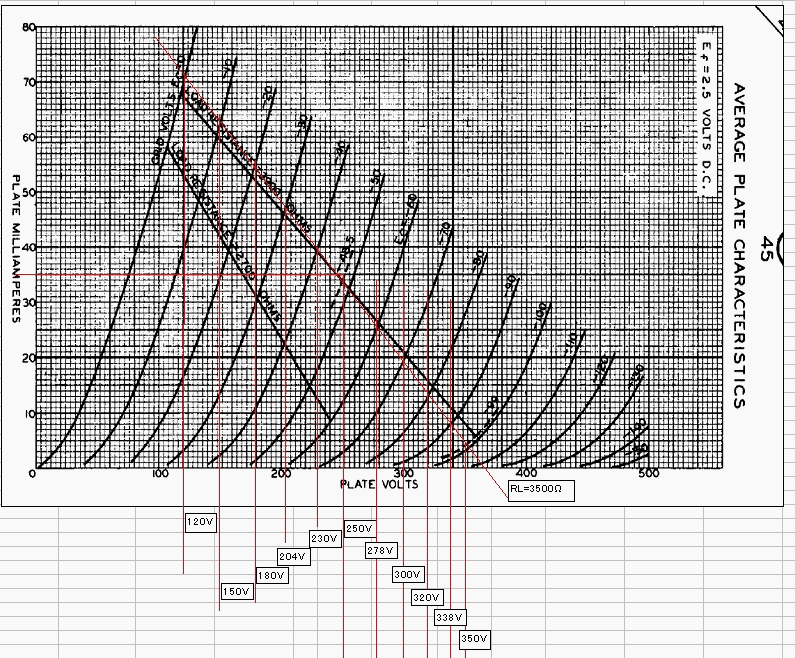
�@���}�̂悤��MS-Excel�Ɏg�p����^��ǂ�Ep�|Ip�����̃O���t���摜�Ƃ��ē\��t���A�z�肷�铮������𗎂Ƃ����݂܂��B
�@���̗�ł́A�^��ǂɂS�T��p���A
RL-3.5�����A�O���b�h�o�C�A�X��-48.5V�AEp=250V�Ōv�Z���܂��B
�i�}�\�P�F�S�T��Ep�\Ip�����Ƀ��[�h���C�����L���j
���ӂ��ׂ��_�F
�@Ep-Ip�����̃O���t����ǂݎ��_�́A�z�肷��O���b�h�d���̍ō��l����Œ�l�܂łȂ�ׂ��ϓ��ɁA�������Ƃ邱�Ƃ��A�덷�̏��Ȃ��ߎ����邽�߂ɏd�v�ł��B�܂��A�O���t����̓ǂݎ�萸�x���d�v�ł��BExcel�ɂ͒������Ђ��ĉE�N���b�N���A�u�I�[�g�V�F�C�v�̏����ݒ�v���u�T�C�Y�v�Ɛi�ނƒ����̒������\�������@�\������A������d���Ɋ��Z����̂ɕ֗��ł����B
�@
�@
Step2�F�O���t��ǂ݁AEg��Ep�̊W��\�ɗ��Ƃ�����
�@����_�̃O���b�h�d���A�v���[�g�d������Ƃ��āA�d���̍����L�����܂��B���̕\�����ɃO���t���쐬���܂��B
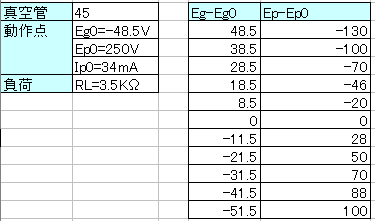
�i�}�\�Q�F���f�[�^�̍쐬�j
�@�@�@
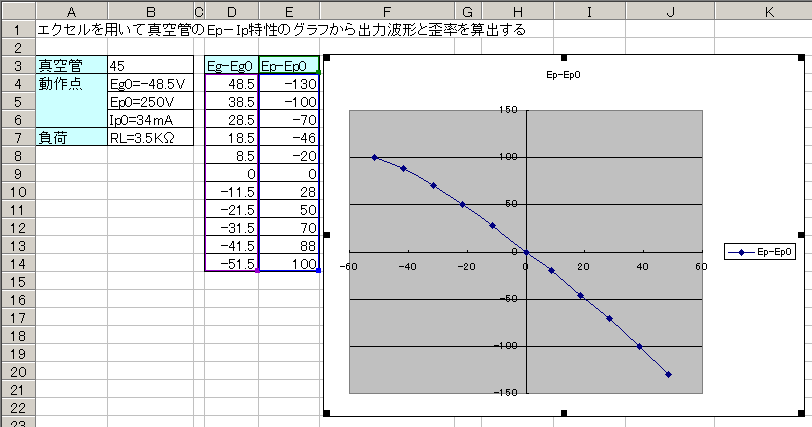
Step3�F�\����O���t���쐬���A�ߎ�����
�}�\�Q�̕\�����ɁAExcel�̃O���t�E�B�U�[�h���U�z�}�Ɛi��ŃO���t�����������܂��B
 �@
�@
�i�}�\�R�F�O���t�̍쐬�j
�@
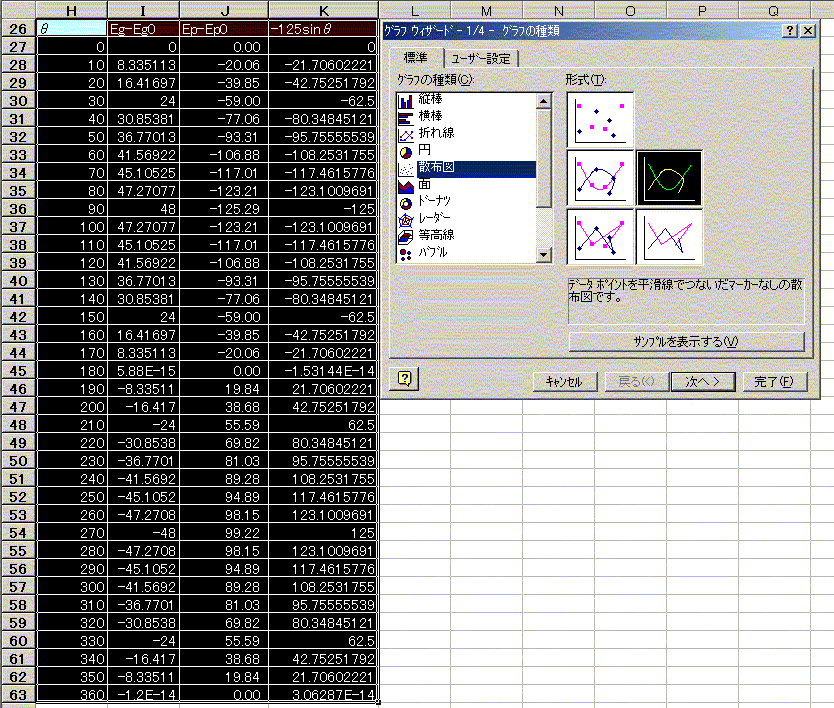
�@���̌�A�O���t�̐����E�N���b�N����ƌ���郁�j���[�̒�����u�ߎ��Ȑ��̒lj��v��I�����܂��B
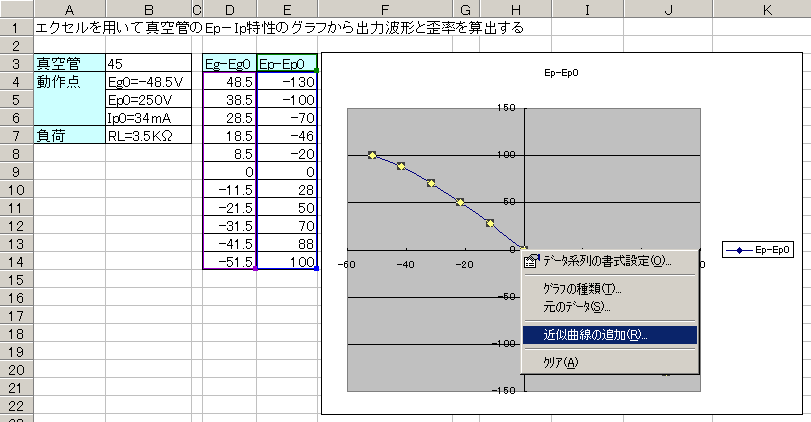
�i�}�\�S�F�ߎ��Ȑ��̒lj��j
�@
�ߎ��Ȑ��̒lj��v�Ƃ����E�C���h�E���o������̂ŁA�u��ށv���N���b�N���A�u�������ߎ��v��I�����A�������U�Ɏw�肵�܂��B�i6���ȉ��ł��ߎ��\�ł��B�j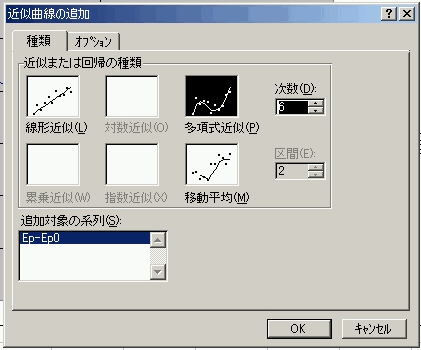 �@
�@
�i�}�\�T�F�u��ށv�̐ݒ�j
�@
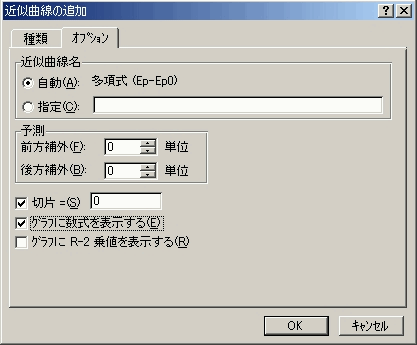
�u�I�v�V�����v���N���b�N���A�u�ؕЁv��0�Ɏw�肷��Ƌ��ɁA�u�O���t�ɐ�����\������v�Ƀ`�F�b�N�����܂��B
 �@
�@
�i�}�\�U�F�u�I�v�V�����v�̐ݒ�j
�@
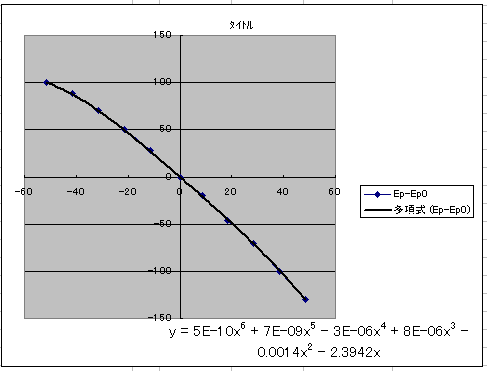
����ƁA�O���t�ɁA�O���t���U�����ŋߎ�������������܂��B���̃O���t�������ɋ߂��^��ǂقǁu���������悢�v�Ƃ������ƂɂȂ�܂��B
 �@
�@
�i�}�\�V�F�ߎ����j
�@
�����œ���ꂽ���l����A
�U����![]() �ɂ����ČW��a�`f�����̕\�̂悤�Ɍ���ł��܂��B
�ɂ����ČW��a�`f�����̕\�̂悤�Ɍ���ł��܂��B
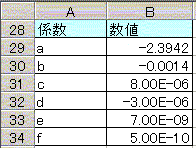
�i�}�\�W�F�W���̕\�j
���̎�
![]() �E�E�E�@
�E�E�E�@
�́A���̐^��ǁi�S�T�j�̓��Y��������ɂ�����O���b�h�d���̕ω��ƃv���[�g�d���̕ω��̊W���U�����ŋߎ��������Ƃ������ƂɂȂ�܂��B���̎��̂��ɎO�p���������邱�ƂŁA�o�͔g�`�̃O���t���쐬���邱�Ƃ�A�����g�c�����v�Z���邱�Ƃ��\�ɂȂ�܂��B
�@�@�@
Step4�F�ߎ��������ƂɁA�����g����͂����ꍇ�̏o�͔g�`���쐬����
�@���}�̂悤�ɐ����g�P�������̕\��Excel�ō쐬���܂��B
Eg-Eg0�̕����͎O�p���isin�Ɓj�ɓ��͓d���i�s�[�N�l�j���悵�����l�AEp-Ep0�̗��́AStep3�œ����@�����@���̗�̏ꍇ�A�O���b�h�o�C�A�X��
48.5V�ł����̂ŃO���b�h���͂̃s�[�N�l�Ƃ���48V��ݒ肵�܂��B��ԉE�̗��͏o�͔g�`�������g����ǂ̂��炢�c��ł��邩���r���邽�߂̎O�p���i���̏ꍇ��-125sin�Ɓj�ł��B�s�[�N�d���ɂ����Ə����ȓd������͂���A���o�͎��̘c�݂̏��Ȃ��ꍇ���݂邱�Ƃ��ł��܂��B�@���Q�l�܂łɁA�}�\�X�̏ꍇ�AJ-27�̃Z���̌v�Z����
=$B$29*I27+$B$30*POWER(I27,2)+$B$31*POWER(I27,3)+$B$32*POWER(I27,4)+$B$33*POWER(I27,5)+$B$34*POWER(I27,6) �ƂȂ��Ă��܂��B
�i�}�\�X�F���́\�o�͂̊W�j
�@
�@�}�\�X�̕\����O���t���쐬���܂��B�\�S�̂���I�����ăO���t�E�B�U�[�h���U�z�}�Ɛi�݁A�O���t���쐬���܂��B
�i�}�\�P�O�F�O���t�̍쐬�j
�@���}�̂悤�ȃO���t���������܂��B�����͐����g����͂����ꍇ�̃O���b�h�d���̕ω��A�s���N�F�̐��̓v���[�g�d���̕ω�������킵�܂��B��r�̂��߂̐����g�͉��F�Ŏ�����Ă��܂��B
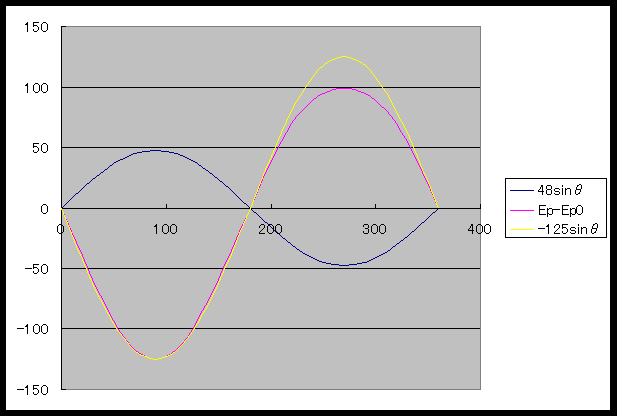
�i�}�\�P�P�F���͓d���Əo�͓d���̊W�j
�@��������p���āA���͔g�`�ɕʂ̐^��ǂ̏o�͔g�`�������邱�Ƃɂ��A�Q�i�����̏ꍇ�̓��o�͓������V�~�����[�V�������邱�Ƃ��ł��܂��B����ɂ��A�V���O���A���v�ł̂Ђ��݂̑ŏ������ʂ��O���t�Ŋm�F���邱�Ƃ��ł��܂��B�@�@
�@
Step5�F�Ђ��ݗ����v�Z����
�@�ߎ��������ƂɁA�����g�c�ݗ����v�Z���邱�Ƃ��ł��܂��B�ߎ������U�����Ƃ����̂ŁA��U�������g�܂Ōv�Z���ł��܂��B
![]() �̏ꍇ�A
�̏ꍇ�A![]() �Ƃ��đ������ƁA
�Ƃ��đ������ƁA
��{�g�����̌W����![]()
![]()
������g�����̌W����![]()
��O�������g�����̌W����![]()
��l�������g�����̌W����![]()
��������g�����̌W����![]()
��Z�������g�����̌W����![]()
�ƂȂ�܂��B
�v�Z���ɂɂ��āA�����Ȃ�܂��̂������������Q�Ƃ��������B�i2005.1.23�v�Z���e���ꕔ�������܂������A�V�~�����[�V�������ʂɂ͉e������܂���B�j
�@���̌��ʂ����Ƃ�Excel�ō����g�c�ݗ����v�Z���܂��B�Ȃ��A�����g�c�ݗ��̌v�Z���́A���̎��ɂ��܂��B
(2006.2.5�c���̒�`������j
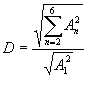 �@�@�@
�@�@�@
�@![]() ��n�������g�i
��n�������g�i![]() �j�ɑΉ�����W���Ƃ���B�i
�j�ɑΉ�����W���Ƃ���B�i![]() �͊�{�g�j
�͊�{�g�j
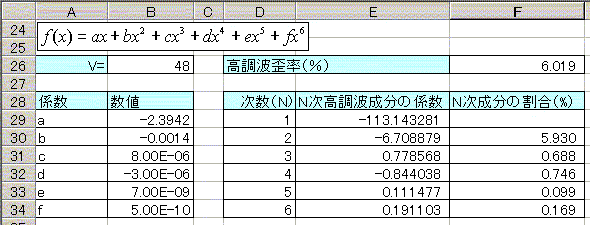
�i�}�\�P�Q�F�c�ݗ��̌v�Z�\�j
���̕\�ŁA
E-29�̃Z���i��{�g�����j�̌v�Z���́@=5/8*B33*POWER(B26,5)+3/4*B31*POWER(B26,3)+B29*B26
E-30�̃Z���i������g�����j�̌v�Z���́@=15/32*B34*POWER(B26,6)+1/2*B32*POWER(B26,4)+1/2*B30*POWER(B26,2)
E-31�̃Z���i��O�������g�����j�̌v�Z���́@=5/16*B33*POWER(B26,5)+1/4*B31*POWER(B26,3)
E-32�̃Z���i��l�������g�����j�̌v�Z���́@=3/16*B34*POWER(B26,6)+1/8*B32*POWER(B26,4)
E-33�̃Z���i��������g�����j�̌v�Z���́@=1/16*B33*POWER(B26,5)
E-34�̃Z���i��Z�������g�����j�̌v�Z���́@=1/32*B34*POWER(B26,6)
�ƂȂ��Ă��܂��B
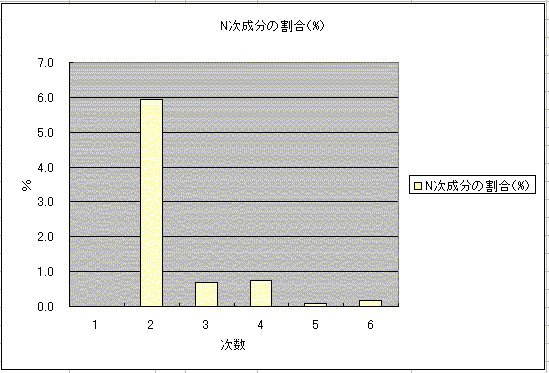
�@�܂��A�}�\�P�Q�̕\�����ƂɁA�O���t���쐬����A�����g�����̊��������邱�Ƃ��ł��܂��B���M�O�Ɋǂ̃V���O���A���v�͋������Ђ��݂������Ƃ����Ă��邱�Ƃ��O���t�̏�ł��m�F�ł��܂��B
 �@
�@
�i�}�\�P�R�F�����g�����̊����j�@�@
�@
������
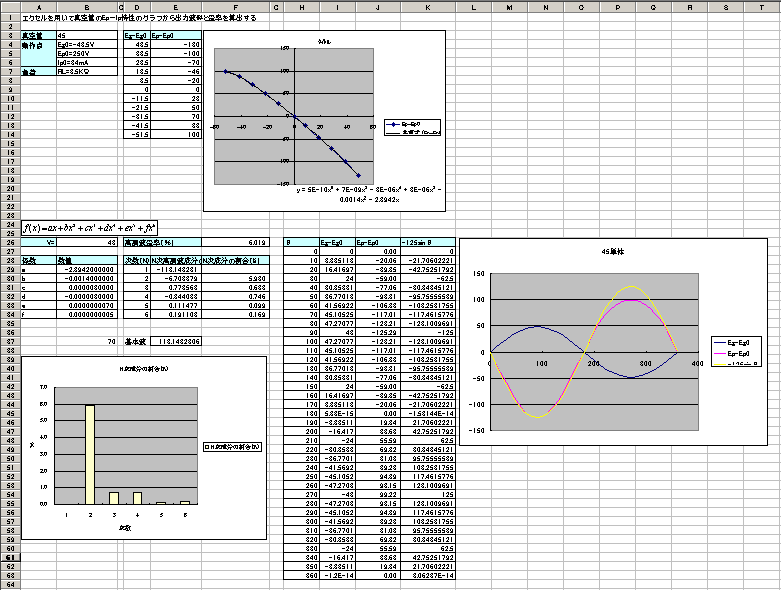
�ȏ�̎菇�ŁA���[�h���C������ǂݎ�鐔�l����Excel�����p���āA�o�͔g�`�̊m�F�Ƙc�ݗ��̌v�Z���ł��܂����B�@��ʑS�̂ł͂��̂悤�ȃ��C�A�E�g�ɂ��܂����B���[�h���C���͕ʂ̃V�[�g�ɓ\��t���܂����B
 �@
�@
�i�}�\�P�S�F�����}�j
�@�ŏ��̓��͂͏��X�ʓ|�ł����A��xExcel�̃V�[�g���쐬���Ă��܂��A���Ƃ̓��[�h���C������̐��l�������͂���Α��̐^��ǂł��ȒP�ɏo�͔g�`�̃V�~�����[�V�����Ƙc�ݗ��̌v�Z���ł��܂��B
�@�R�ɊǂƂT�Ɋǂ̘c�ݐ����̈Ⴂ�ȂǁA���ۂɎ����Ă݂�Ƃ������낢�ł��B�c�݂����Ȃ��Ȃ镉�ׂ�I��A�O�q�̒ʂ�O�i�̏o�͂�����Ɋ��ɓ��͂��Ęc�݂̑ŏ��������������蓙�A��H�̐v�ɉ��p�ł��܂����A��Ԗ��ɗ��̂́A���[�h���C�����������̊��������ތP���ɂȂ邱�Ƃ��Ǝv���܂��B
�@���Q�l�܂ł�6BM8�̂T�ɊǕ��ɂ��āAEp=200V ,Esg=200V,Eg=-16V,RL=5.6K���Ƃ��������œ��l�̃V�~�����[�V�����������Ȃ������ʂ̃O���t���������������B
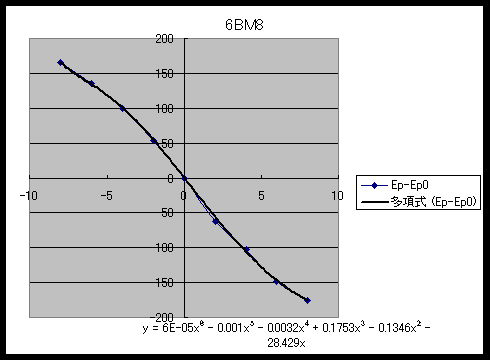
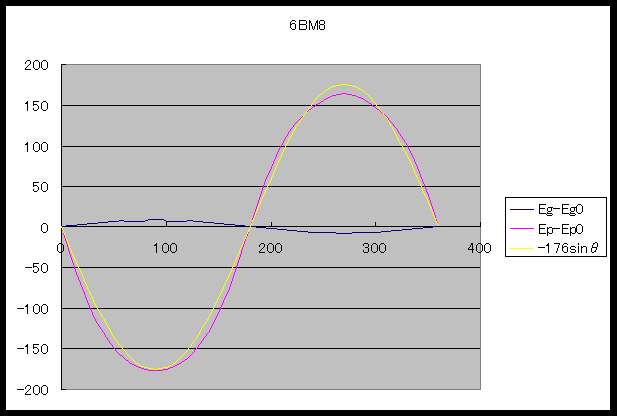
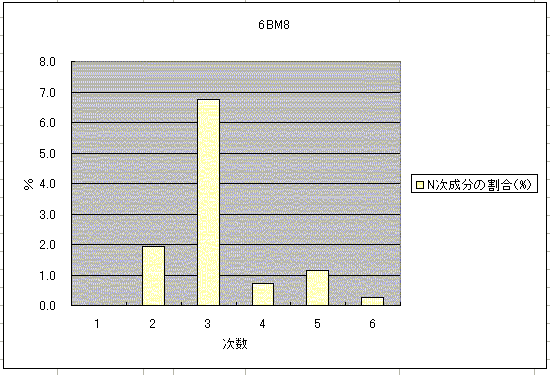
�@���M�O�Ɋǂ�45�ɔ�ׂ�6BM8�̌܋ɊǕ��͊���̘c�݂��������Ƃ��킩��܂��B
�@����A�H�t���ň�{�W��~��45�i���Áj���Փ��������Ă��܂����������A����ȃO���t�����Ȃ���[�������Ă��܂��B�̐S��45�V���O���A���v�̕��́A���ԂƂ����������Ȃ��ĂȂ��Ȃ�����ɂƂ肩����܂���B�@�@
�@
�Q�l�����F
�ؑ��N���@�w��M�̐^��ǃA���v�x�A���{���Əo�ŎЁA2004�N
�ؑ��N���̃z�[���y�[�W�w��M�̐^��ǁx
http://home.highway.ne.jp/teddy/tubes/tubes.htm���[�h���C���̈������ɂ��Ċw�т܂����B
�@
�u�ꁗ���Ύ��z�[���y�[�W
�w�I�[�f�B�I�̉Ȋw�x�̂Ȃ��́w�����Ƙc�x�̃y�[�W
http://www.ne.jp/asahi/shiga/home/MyRoom/Audio.htm
http://www.ne.jp/asahi/shiga/home/MyRoom/distortion.htm���͂Əo�͂̊W�𑽍����ŕ\���A�C�f�A���w�т܂����B
�@
�����Z�p�Ȋw��w�@�����q�H�w�������@��E�ؑ��������z�[���y�[�W
�wExcel��p�����ŏ����@�x
http://carbo.nagaokaut.ac.jp/suzukilab/default.html
http://carbo.nagaokaut.ac.jp/suzukilab/2nd-grade-excel/excel-least-square.htmlExcel�̃O���t����ߎ����������@�͂��̃y�[�W����w�т܂����B
�@
Frank Philipse���̃z�[���y�[�W
�wFrank's Electron tube Pages�x
http://home.wxs.nl/~frank.philipse/frank/frank.html
�^��ǂ̓����f�[�^���L�x�ł��B