2005擭2寧7擔廋惓
2006擭8寧21擔廋惓
HARU仐朙嫶
侾丏偼偠傔偵
俀丏柍婣娨忬懺偺懡崁幃傪摼傞
俁丏懡崁幃傪尦偵Excel偺昞傪嶌惉偡傞
係丏晧婣娨傪偐偗偨応崌偺懡崁幃傪摼傞
俆丏弌椡攇宍偲崅挷攇榗棪傪寁嶼偡傞
丂擖椡揹埑傪倶丄弌椡揹埑傪f(x)偲偟偨偲偒丄
丂慺恖偺峫偊偨帺屓棳偱偡偺偱丄峫偊堘偄側偳偁傞偐傕抦傟傑偣傫丅偍婥偯偒偺嵺偼偛嫵帵婅偄偨偄偲懚偠傑偡丅
丂晧婣娨傪偐偗傞妱崌乮弌椡揹埑傪擖椡偵媡憡偱壛偊傞揹埑偺弌椡揹埑偵懳偡傞妱崌乯傪t乮t亜0)偲偟傑偡丅晧婣娨傪偐偗偨帪偺弌 椡揹埑偑y丄擖椡揹埑傪x' 丄晧婣娨傪偐偗側偄応崌偵弌椡揹埑偑y偲側傞擖椡揹埑傪x偲偡傞偲丄x'偲倷偵偼埲壓偺娭學偑惉棫偟偰偄傑偡丅
y=f(x'+ty) 丂y=f(x)丂丂偟偨偑偭偰丄丂x=x'+ty
廬偭偰丄x'偲x,y,t偺娭學偼丄
x'=x-ty丒丒丒嘆
(2006.8.21丗 倲偺抣傪t>0偲偡傞偙偲偱悢幃傪廋惓乯
丂偡偱偵丄柍婣娨忬懺偱偺悢幃f(x)偐傜丄擖椡揹埑偲偟偰憐掕偝傟傞斖埻偺擟堄偺x偵偮偄偰柍婣娨帪偺弌椡揹埑f(x)傪摼傞偙偲偑偱偒傑偡丅 偙傟傪傕偲偵偟偰丄晧婣娨傪偐偗偨応崌偺擖椡x乫偲弌椡偺娭學幃g(x乫)傪媮傔傞偙偲偲偟傑偡丅
丂x'偲y偺娭學傪帵偡曽掱幃傪摫偔曽朄傪峫偊傛偆偲偟偨偺偱偡偑丄擄偟偔偰庤偵偍偊傑偣傫丅偦偙偱丄崱夞傕Excel偺僌儔僼偐傜嬤帡懡崁幃傪 摼傞曽朄傪墳梡偟傑偡丅
丂柍婣娨帪偺擖椡偲弌椡偺娭學傪帵偡僌儔僼忋偺偄偔偮偐偺揰偵偮偄偰丄弌椡揹埑y偑摼傜傟偰偄傟偽丄晧婣娨傪偐偗偨応崌偵y傪摼傞偨傔偵昁梫側擖 椡揹埑x乫傪摼傞偙偲偼丄嘆幃傪梡偄偰娙扨偵偱偒傑偡丅
丂偡偱偵丄f(x)偵偮偄偰偼丄僌儔僼傪摼傞偙偲偑偱偒偰偄傑偡偺偱丄僌儔僼忋偺偄偔偮偐偺揰乮側傞傋偔峀偄斖埻偐偮懡偔偺揰偑朷傑偟偄偱偡丅乯 偵偮偄偰丄晧婣娨傪偐偗偨応崌偺擖椡揹埑曄壔x'偲懳墳偡傞僾儗乕僩揹埑偺曄壔倷偺慻傪摼傞偙偲偑偱偒傑偡丅
丂偦偟偰丄MS-Excel偺婡擻傪妶梡偟偰丄偙傟傜偺揰偐傜嶶晍恾傪嶌惉偟丄嬤帪懡崁幃傪摼傞偙偲偑偱偒傑偡丅偙偺嬤帪懡崁幃偑晧婣娨傪偐偗偨 応崌偺擖椡x'偲弌椡y偺娭學幃y=g(x乫)偲偄偆偙偲偵側傝傑偡丅
丂埲壓丄愝寁丒惢嶌拞偺45僔儞僌儖傾儞僾偺椺傪戣嵽偵丄晧婣娨傪偐偗偰傒偨応崌偺擖椡揹埑偲弌椡揹埑偺娭學幃傪媮傔偰傒傑偡丅
丂45僔儞僌儖傾儞僾乮愝寁曇乯傛傝丄76-76-45偺嶰抜憹暆偺傾儞僾乮柍婣 娨乯偺弶抜擖椡偲弌椡抜偺僾儗乕僩揹埑偺娭學偼丄
偲側傝傑偡丅乮弌椡抜RL=3.5K兌偺応崌乯
丂偙偺幃傪摼傞曽朄偵偮偄偰偼丄偙偪傜偲偙 偪傜傪偛嶲徠偔偩偝偄丅
丂偙偺昞偺傛偆偵丄擖椡乮76弶抜傊偺擖椡揹埑偺曄壔乯偲弌椡乮45偺僾儗乕僩揹埑偺曄壔乯偺娭學傪Excel偺昞偵擖椡偟傑偡丅弌椡揹埑偺曄壔 傪帵偡娭悢偼丄俀丏偱摼傜傟偨懡崁幃偺學悢傪梡偄傟偽丄
丂嘇幃傪梡偄偰丄擖椡揹埑x傪-0.46V偐傜+0.46V偺斖埻偱曄壔偝偣偨昞傪Excel傪梡偄偰嶌惉偟傑偡丅億僀儞僩偼懡偄傎偆偑傛傝惓妋 側嬤帡幃偑摼傜傟傞偼偢偱偡丅乮偙偺椺偱偼38億僀儞僩乯奺乆偺x偵懳偟偰y偼嘇幃偱媮傔傞偙偲偑偱偒傑偡丅傑偨丄x'傕嘆幃偵傛傝寁嶼偱偒傑 偡丅廬偭偰丄Excel偺婡擻傪梡偄傞偙偲偵傛傝丄掕悢t傪掕傔丄x傪擖椡偡傟偽丄x'偲y偼帺摦揑偵擖椡偱偒傑偡丅
丂壓偺昞偱丄掕悢倲偼丄45偺僾儗乕僩揹埑偺曄壔偵懳偡傞婣娨揹埑偺妱崌傪偁傜傢偟傑偡丅t偺抣偼弌椡僩儔儞僗偵傛傞曄埑偺抣偲婣娨掞峈偵傛傞暘 埑偱寛傑傝傑偡丅偙偺応崌丄弌椡僩儔儞僗偼3.5K兌丗8僆乕儉側偺偱丄3500/8亖437.5丅

丂俁丏偱摼傜傟偨昞偐傜丄x'偲y偺憡娭恾傪Excel偺僌儔僼僂傿僓乕僪傪梡偄偰嶶晍恾傪嶌惉偟丄偙偺僌儔僼傪尦偵嬤帡懡崁幃傪摼傑偡丅
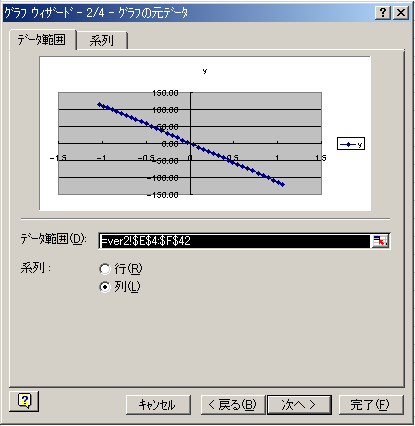
摼傜傟偨嶶晍恾偐傜嬤帡嬋慄傪摼傑偡丅
懡崁幃嬤帡傪慖戰偟丄師悢傪嵟戝偺俇偲偟傑偡丅

乽僆僾僔儑儞乿僞僽傪僋儕僢僋偟丄嬤帡嬋慄偺懡崁幃傪摼傑偡丅

偙傟偱姰惉偱偡丅
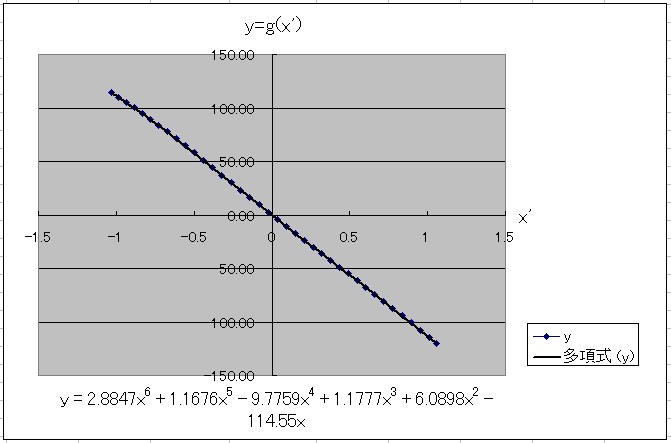
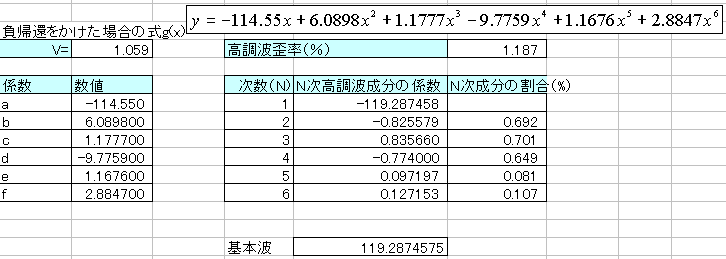
丂係丏偱摼傜傟偨俇師偺懡崁幃
丂側偍丄偙偺幃偼丄偁偔傑偱嬤帡幃偱偡偺偱丄億僀儞僩偺偲傝偐偨偵傛偭偰懡彮偺岆嵎傪惗偠傑偡丅2捠傝乮傕偆堦曽偼19揰偱寁嶼偟傑偟偨丅乯偺傗 傝偐偨偱帋偟偰傒偨偲偙傠丄6師娭悢偺奺學悢偺堘偄偑嵟戝偱俁丏俁俇亾惗偠傑偟偨偑丄崅挷攇榗棪偺寁嶼寢壥偺嵎偼丄0.001亾偱偟偨偺偱丄幚梡 忋偼栤戣側偄偲峫偊偰偄傑偡丅
丂偙偺幃偑偁傟偽丄偁偲偼丄暿宖乽MS-Excel傪梡偄偰恀嬻娗偺Ep-Ip摿惈恾偐 傜弌椡攇宍偲崅挷攇榗棪傪寁嶼偡傞乿偵婰嵹偟偨庤朄傪梡偄偰丄弌椡攇宍偲崅挷攇榗棪傪寁嶼偡傞偙偲偑偱偒傑偡丅埲壓寢壥偺傒傪偛棗偔 偩偝偄丅


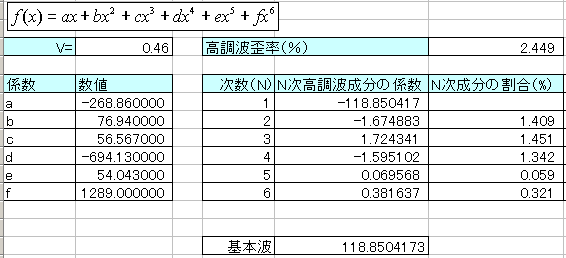
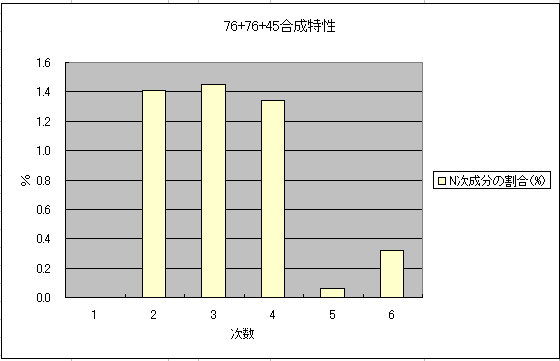
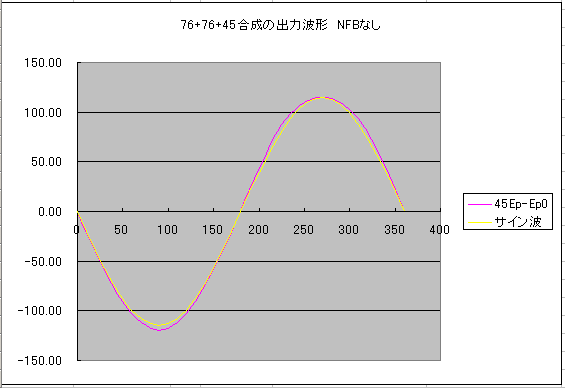
丂偛嶲峫傑偱偵丄摨偠夞楬偱晧婣娨傪偐偗側偄応崌偺崅挷攇榗棪偲弌椡攇宍偺僌儔僼偼埲壓偺傛偆偵側傝傑偟偨丅偳偪傜傕弌椡偑栺俀W偲側傞擖椡揹埑 偱偺斾妑偱偡丅
丂NFB傪偐偗傞偙偲偱丄僎僀儞偑栺敿暘偵側偭偰偄傑偡偑丄偦偺暘丄崅挷攇榗棪偼2.448%偐傜1.187亾偵尭彮偡傞偙偲偑傢偐傝傑偡丅幚嵺 偺惢嶌偱偙偺傛偆側寢壥偑偊傜傟傞偐偳偆偐妝偟傒偱偡丅
偙偺儁乕僕偺嵟弶偵栠傞
僩僢僾儁乕僕偵栠傞